Agamah, Francis E., Jumamurat R. Bayjanov, Anna Niehues, Kelechi F. Njoku, Michelle Skelton, Gaston K. Mazandu, Thomas H. A. Ederveen, Nicola Mulder, Emile R. Chimusa, and Peter A. C. ’t Hoen. 2022.
“Computational Approaches for Network-Based Integrative Multi-Omics Analysis.” Frontiers in Molecular Biosciences 9 (November): 967205.
https://doi.org/10.3389/fmolb.2022.967205.
Andres, Axel, Aldo Montano-Loza, Russell Greiner, Max Uhlich, Ping Jin, Bret Hoehn, David Bigam, James Andrew Mark Shapiro, and Norman Mark Kneteman. 2018.
“A Novel Learning Algorithm to Predict Individual Survival After Liver Transplantation for Primary Sclerosing Cholangitis.” Edited by Yinglin Xia.
PLOS ONE 13 (3): e0193523.
https://doi.org/10.1371/journal.pone.0193523.
Antolini, Laura, Patrizia Boracchi, Elia Biganzoli, L Antolini, P Boracchi, and E Biganzoli. 2005.
“A time-dependent discrimination index for survival data.” Statistics in Medicine 24 (24): 3927–44.
https://doi.org/10.1002/SIM.2427.
Avati, Anand, Tony Duan, Sharon Zhou, Kenneth Jung, Nigam H Shah, and Andrew Y Ng. 2020.
“Countdown Regression: Sharp and Calibrated Survival Predictions.” In
Proceedings of the 35th Uncertainty in Artificial Intelligence Conference, edited by Ryan P Adams and Vibhav Gogate, 115:145–55. Proceedings of Machine Learning Research. PMLR.
https://proceedings.mlr.press/v115/avati20a.html.
Binder, Harald, and Martin Schumacher. 2008.
“Adapting Prediction Error Estimates for Biased Complexity Selection in High-Dimensional Bootstrap Samples.” Statistical Applications in Genetics and Molecular Biology 7 (1).
https://doi.org/10.2202/1544-6115.1346.
Blanche, Paul, Michael W Kattan, and Thomas A Gerds. 2019.
“The c-index is not proper for the evaluation of t-year predicted risks.” Biostatistics 20 (2): 347–57.
https://doi.org/10.1093/biostatistics/kxy006.
Bommert, Andrea, and Michel Lang. 2021.
“stabm: Stability Measures for Feature Selection.” Journal of Open Source Software 6 (59): 3010.
https://doi.org/10.21105/joss.03010.
Breheny, Patrick, and Jian Huang. 2015. “Group Descent Algorithms for Nonconvex Penalized Linear and Logistic Regression Models with Grouped Predictors.” Statistics and Computing 25: 173–87.
Breheny, Patrick, Yaohui Zeng, and Ryan Kurth. 2021.
“Grpreg: Regularization Paths for Regression Models with Grouped Covariates.” R Package Version 3.4.0. https://CRAN.R-project.org/package=grpreg (23 January 2023, date last accessed).
Chu, Jiadong et al. 2022.
“The Application of Bayesian Methods in Cancer Prognosis and Prediction.” Cancer Genom. Proteom. 19 (1): 1–11.
https://doi.org/10.21873/cgp.20298.
Friedman, Jerome, Trevor Hastie, and Robert Tibshirani. 2010.
“Regularization Paths for Generalized Linear Models via Coordinate Descent.” Journal of Statistical Software 33 (1): 1–22.
https://doi.org/10.18637/jss.v033.i01.
Graf, Erika, Claudia Schmoor, Willi Sauerbrei, and Martin Schumacher. 1999.
“Assessment and comparison of prognostic classification schemes for survival data.” Statistics in Medicine 18: 2529–45.
https://doi.org/10.1002/(SICI)1097-0258(19990915/30)18:17/18.
Haider, Humza, Bret Hoehn, Sarah Davis, and Russell Greiner. 2020.
“Effective Ways to Build and Evaluate Individual Survival Distributions.” Journal of Machine Learning Research 21 (85): 1–63.
http://jmlr.org/papers/v21/18-772.html.
Harrell, Frank E., Robert M. Califf, David B. Pryor, Kerry L. Lee, and Robert A. Rosati. 1982.
“Evaluating the Yield of Medical Tests.” JAMA: The Journal of the American Medical Association 247 (18): 2543–46.
https://doi.org/10.1001/jama.1982.03320430047030.
Hasin, Yehudit, Marcus Seldin, and Aldons Lusis. 2017.
“Multi-Omics Approaches to Disease.” Genome Biol. 18 (August): 83.
https://doi.org/10.1186/s13059-017-1215-1.
Heagerty, Patrick J., and Yingye Zheng. 2005.
“Survival Model Predictive Accuracy and ROC Curves.” Biometrics 61 (1): 92–105.
https://doi.org/10.1111/J.0006-341X.2005.030814.X.
Herrmann, Moritz et al. 2021.
“Large-Scale Benchmark Study of Survival Prediction Methods Using Multi-Omics Data.” Brief. Bioinform. 22 (3): bbaa167.
https://doi.org/10.1093/bib/bbaa167.
Ickstadt, Katja, Martin Schäfer, and Manuela Zucknick. 2018.
“Toward Integrative Bayesian Analysis in Molecular Biology.” Annual Review of Statistics and Its Application 5 (1): 141–67.
https://doi.org/10.1146/annurev-statistics-031017-100438.
John, Christopher R, David Watson, Dominic Russ, Katriona Goldmann, Michael Ehrenstein, Costantino Pitzalis, Myles Lewis, and Michael Barnes. 2020.
“M3C: Monte Carlo Reference-Based Consensus Clustering.” Scientific Reports 10 (1): 1816.
https://doi.org/10.1038/s41598-020-58766-1.
Kang, Mingon, Euiseong Ko, and Tesfaye B Mersha. 2022.
“A Roadmap for Multi-Omics Data Integration Using Deep Learning.” Briefings in Bioinformatics 23 (1): bbab454.
https://doi.org/10.1093/bib/bbab454.
Karimi, Mohammad Reza, Amir Hossein Karimi, Shamsozoha Abolmaali, Mehdi Sadeghi, and Ulf Schmitz. 2022.
“Prospects and Challenges of Cancer Systems Medicine: From Genes to Disease Networks.” Briefings in Bioinformatics 23 (1): bbab343.
https://doi.org/10.1093/bib/bbab343.
Lang, Michel, Martin Binder, Jakob Richter, Patrick Schratz, Florian Pfisterer, Stefan Coors, Quay Au, Giuseppe Casalicchio, Lars Kotthoff, and Bernd Bischl. 2019.
“mlr3: A modern object-oriented machine learning framework in R.” Journal of Open Source Software 4 (44): 1903.
https://doi.org/10.21105/JOSS.01903.
Lee, Kyu Ha, Sounak Chakraborty, and Jianguo Sun. 2015.
“Survival Prediction and Variable Selection with Simultaneous Shrinkage and Grouping Priors.” Stat. Anal. Data Min. 8 (2): 114–27.
https://doi.org/10.1002/sam.11266.
———. 2021.
“psbcGroup: Penalized Parametric and Semiparametric Bayesian Survival Models with Shrinkage and Grouping Priors.” R Package Version 1.5. https://CRAN.R-project.org/package=psbcGroup (23 January 2023, date last accessed).
Love, Michael I., Wolfgang Huber, and Simon Anders. 2014.
“Moderated Estimation of Fold Change and Dispersion for RNA-Seq Data with DESeq2.” Genome Biology 15: 550.
https://doi.org/10.1186/s13059-014-0550-8.
Madjar, Katrin et al. 2021.
“Combining Heterogeneous Subgroups with Graph-Structured Variable Selection Priors for Cox Regression.” BMC Bioinformatics 22: 586.
https://doi.org/10.1186/s12859-021-04483-z.
Mounir, Marta AND Silva, Mohamed AND Lucchetta. 2019.
“New Functionalities in the TCGAbiolinks Package for the Study and Integration of Cancer Data from GDC and GTEx.” PLOS Computational Biology 15 (3): 1–18.
https://doi.org/10.1371/journal.pcbi.1006701.
Nogueira, Sarah, Konstantinos Sechidis, and Gavin Brown. 2018.
“On the Stability of Feature Selection Algorithms.” Journal of Machine Learning Research 18 (174): 1–54.
http://jmlr.org/papers/v18/17-514.html.
Parker, Joel S., Michael Mullins, Maggie C. U. Cheang, Samuel Leung, David Voduc, Tammi Vickery, Sherri Davies, et al. 2009.
“Supervised Risk Predictor of Breast Cancer Based on Intrinsic Subtypes.” Journal of Clinical Oncology 27 (8): 1160–67.
https://doi.org/10.1200/JCO.2008.18.1370.
Sill, Martin, Thomas Hielscher, Natalia Becker, and Manuela Zucknick. 2014.
“c060: Extended Inference with Lasso and Elastic-Net Regularized Cox and Generalized Linear Models.” Journal of Statistical Software 62 (5): 1–22.
https://doi.org/10.18637/jss.v062.i05.
Simon, Noah et al. 2013.
“A Sparse-Group Lasso.” J. Comput. Graph Stat. 22 (2): 231–45.
https://doi.org/10.1080/10618600.2012.681250.
Simon, Noah, Jerome Friedman, Trevor Hastie, and Rob Tibshirani. 2019.
“SGL: Fit a GLM (or Cox Model) with a Combination of Lasso and Group Lasso Regularization.” R Package Version 1.3. https://CRAN.R-project.org/package=SGL (23 January 2023, date last accessed).
Simon, Richard M., Jyothi Subramanian, Ming-Chung Li, and Supriya Menezes. 2011.
“Using cross-validation to evaluate predictive accuracy of survival risk classifiers based on high-dimensional data.” Briefings in Bioinformatics 12 (3): 203–14.
https://doi.org/10.1093/bib/bbr001.
Sonabend, Raphael. 2022.
“Scoring Rules in Survival Analysis.” https://arxiv.org/abs/2212.05260.
Sonabend, Raphael, Franz J. Király, Andreas Bender, Bernd Bischl, and Michel Lang. 2021.
“mlr3proba: an R package for machine learning in survival analysis.” Bioinformatics 37 (17): 2789–91.
https://doi.org/10.1093/BIOINFORMATICS/BTAB039.
Subramanian, Indhupriya, Srikant Verma, Shiva Kumar, Abhay Jere, and Krishanpal Anamika. 2020.
“Multi-Omics Data Integration, Interpretation, and Its Application.” Bioinformatics and Biology Insights 14 (January): 117793221989905.
https://doi.org/10.1177/1177932219899051.
Uno, Hajime, Tianxi Cai, Michael J. Pencina, Ralph B. D’Agostino, and L. J. Wei. 2011.
“On the C-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data.” Statistics in Medicine 30 (10): 1105–17.
https://doi.org/10.1002/SIM.4154.
Uno, Hajime, Tianxi Cai, Lu Tian, and L. J. Wei. 2007.
“Evaluating Prediction Rules for t-Year Survivors With Censored Regression Models.” Journal of the American Statistical Association 102 (478): 527–37.
https://doi.org/10.1198/016214507000000149.
Vandereyken, Katy, Alejandro Sifrim, Bernard Thienpont, and Thierry Voet. 2023.
“Methods and Applications for Single-Cell and Spatial Multi-Omics.” Nature Reviews Genetics 24 (8): 494–515.
https://doi.org/10.1038/s41576-023-00580-2.
Wissel, David, Daniel Rowson, and Valentina Boeva. 2023.
“Systematic Comparison of Multi-Omics Survival Models Reveals a Widespread Lack of Noise Resistance.” Cell Reports Methods 3 (4): 100461.
https://doi.org/10.1016/j.crmeth.2023.100461.
Yan, Jingwen, Shannon L Risacher, Li Shen, and Andrew J. Saykin. 2018.
“Network Approaches to Systems Biology Analysis of Complex Disease: Integrative Methods for Multi-Omics Data.” Briefings in Bioinformatics 19 (6): 1370–81.
https://doi.org/10.1093/bib/bbx066.
Yi, Nengjun, Zaixiang Tang, Xinyan Zhang, and Boyi Guo. 2019.
“BhGLM: Bayesian hierarchical GLMs and survival models, with applications to genomics and epidemiology.” Bioinformatics 35 (8): 1419–21.
https://doi.org/10.1093/bioinformatics/bty803.
Zhao, Yingdong, Ming-Chung Li, Mariam M. Konate, Li Chen, Biswajit Das, Chris Karlovich, P. Mickey Williams, Yvonne A. Evrard, James H. Doroshow, and Lisa M. McShane. 2021.
“TPM, FPKM, or Normalized Counts? A Comparative Study of Quantification Measures for the Analysis of RNA-Seq Data from the NCI Patient-Derived Models Repository.” Journal of Translational Medicine 19 (1): 269.
https://doi.org/10.1186/s12967-021-02936-w.
Zhao, Zhi, John Zobolas, Manuela Zucknick, and Tero Aittokallio. 2024.
“Tutorial on survival modeling with applications to omics data.” Bioinformatics, March.
https://doi.org/10.1093/bioinformatics/btae132.
Zhao, Zhi, Manuela Zucknick, Maral Saadati, and Axel Benner. 2023.
“Penalized Semiparametric Bayesian Survival Models.” R Package Version 2.0.4. https://CRAN.R-project.org/package=psbcSpeedUp.
Zucknick, Manuela, Sylvia Richardson, and Euan A Stronach. 2008.
“Comparing the Characteristics of Gene Expression Profiles Derived by Univariate and Multivariate Classification Methods.” Statistical Applications in Genetics and Molecular Biology 7 (1).
https://doi.org/doi:10.2202/1544-6115.1307.
Zucknick, Manuela, Maral Saadati, and Axel Benner. 2015.
“Nonidentical twins: Comparison of frequentist and Bayesian lasso for Cox models.” Biometrical Journal 57 (6): 959–81.
https://doi.org/10.1002/bimj.201400160.
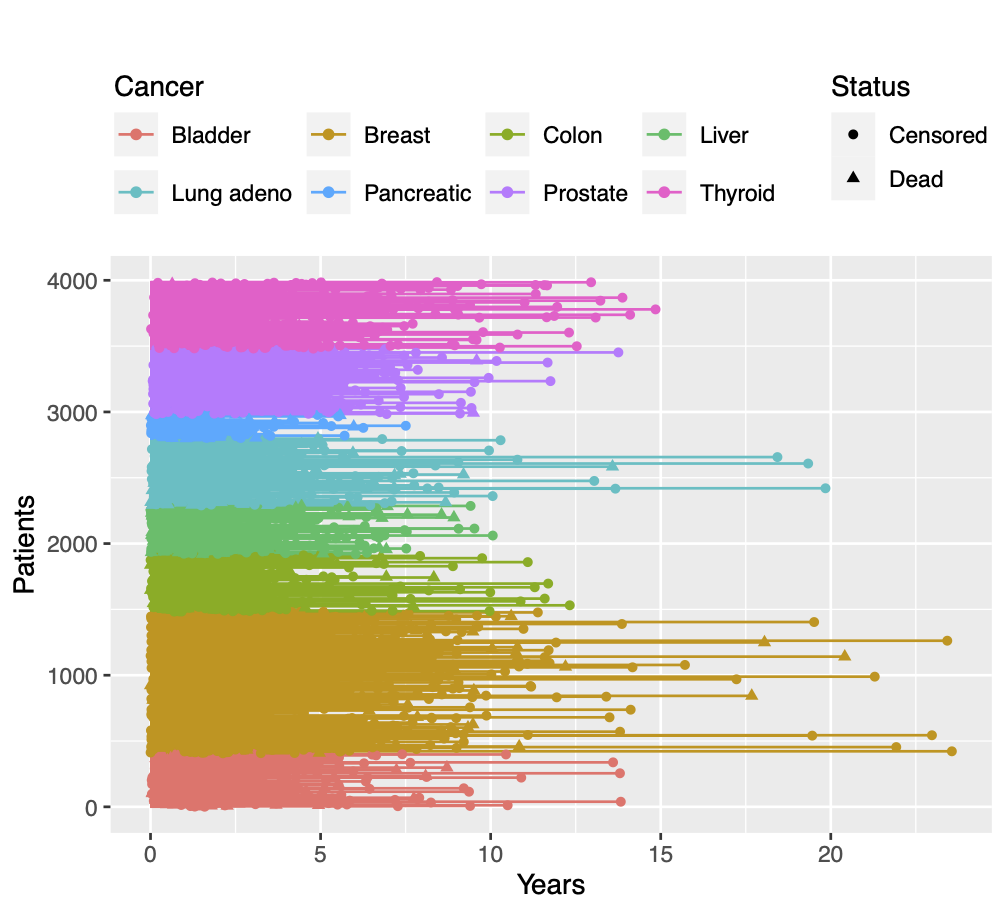
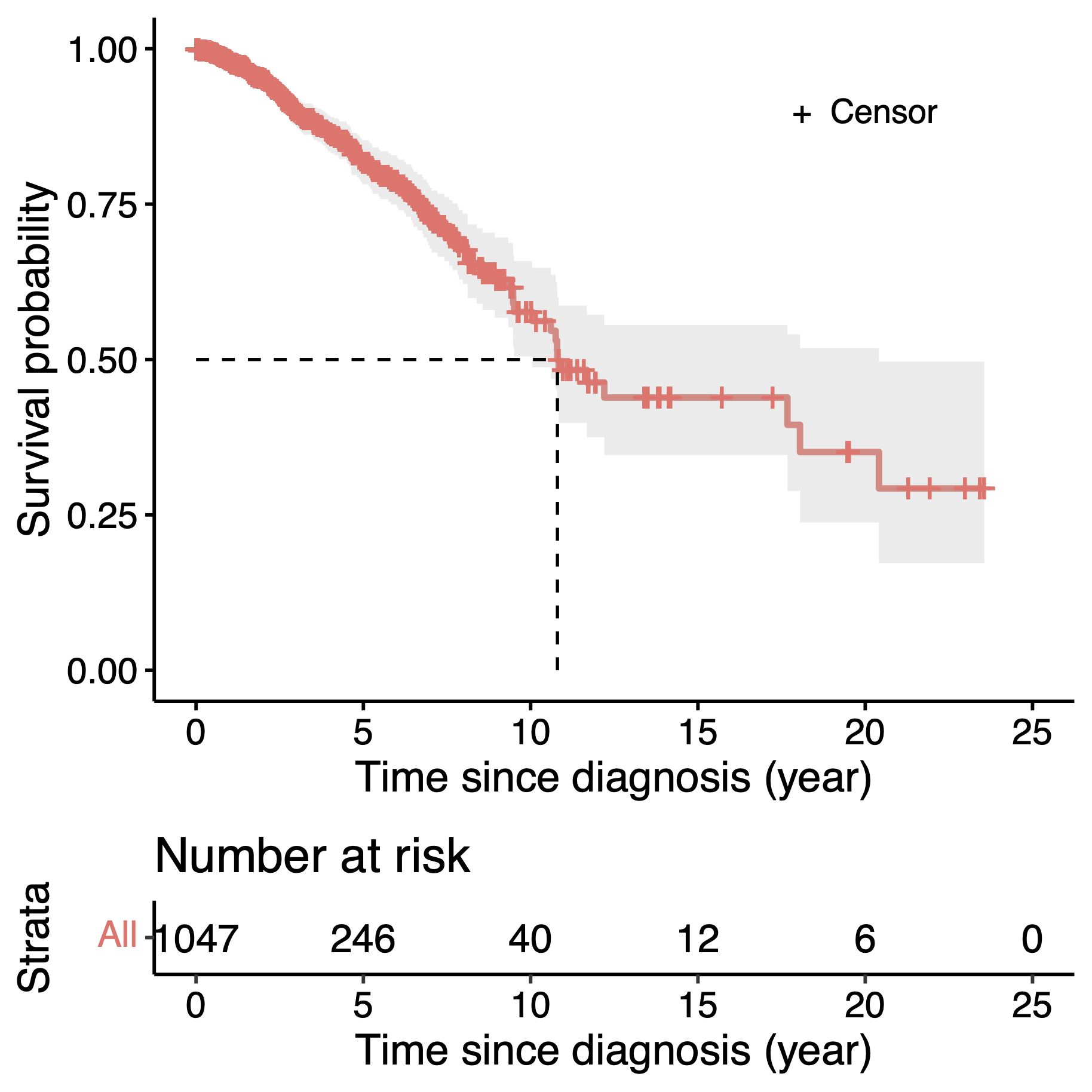
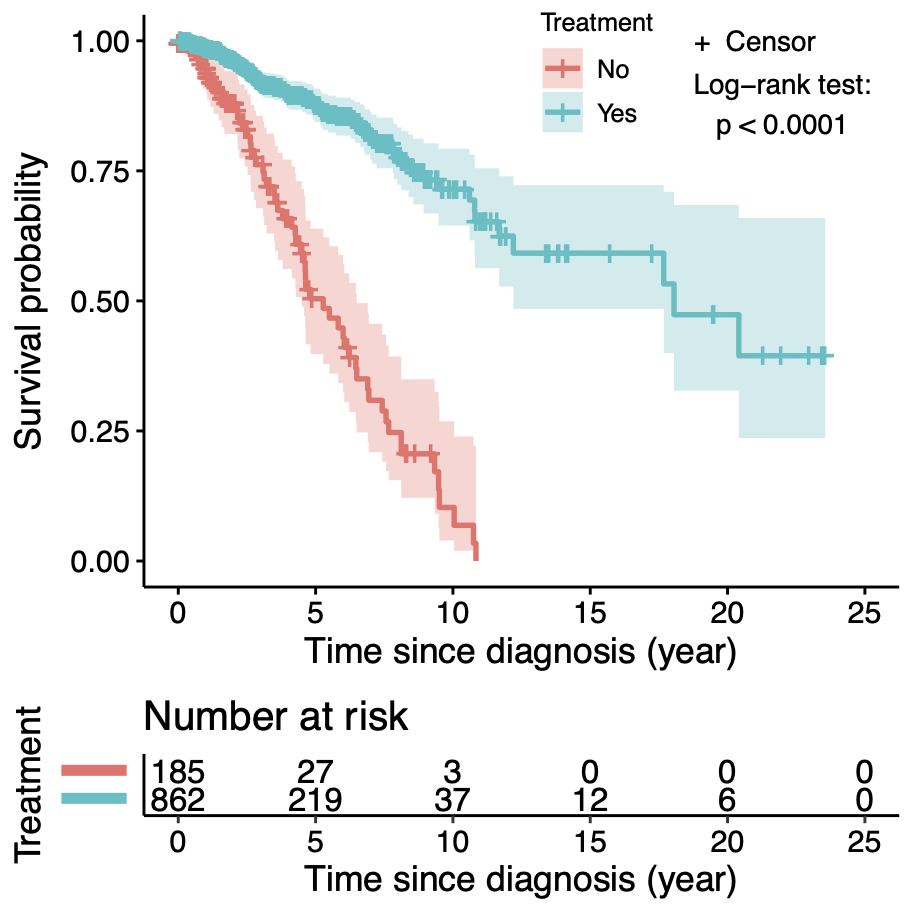
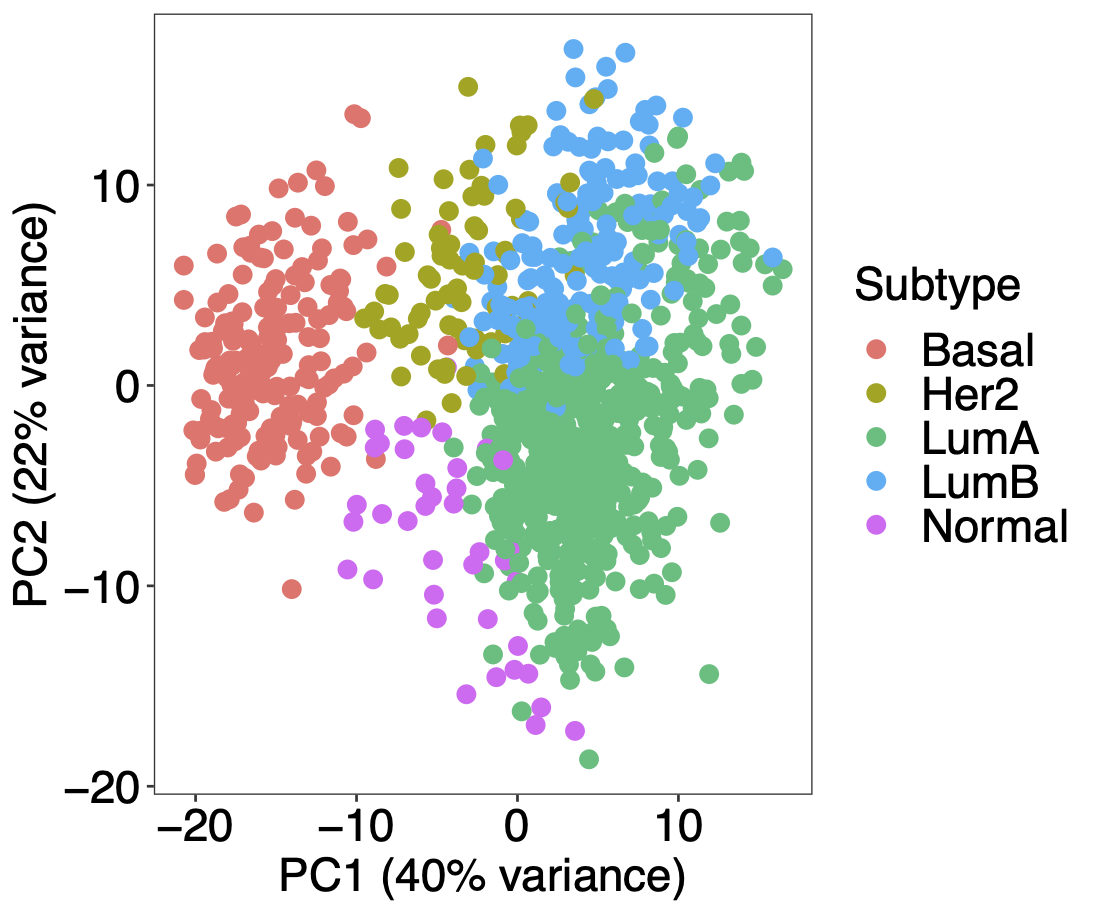
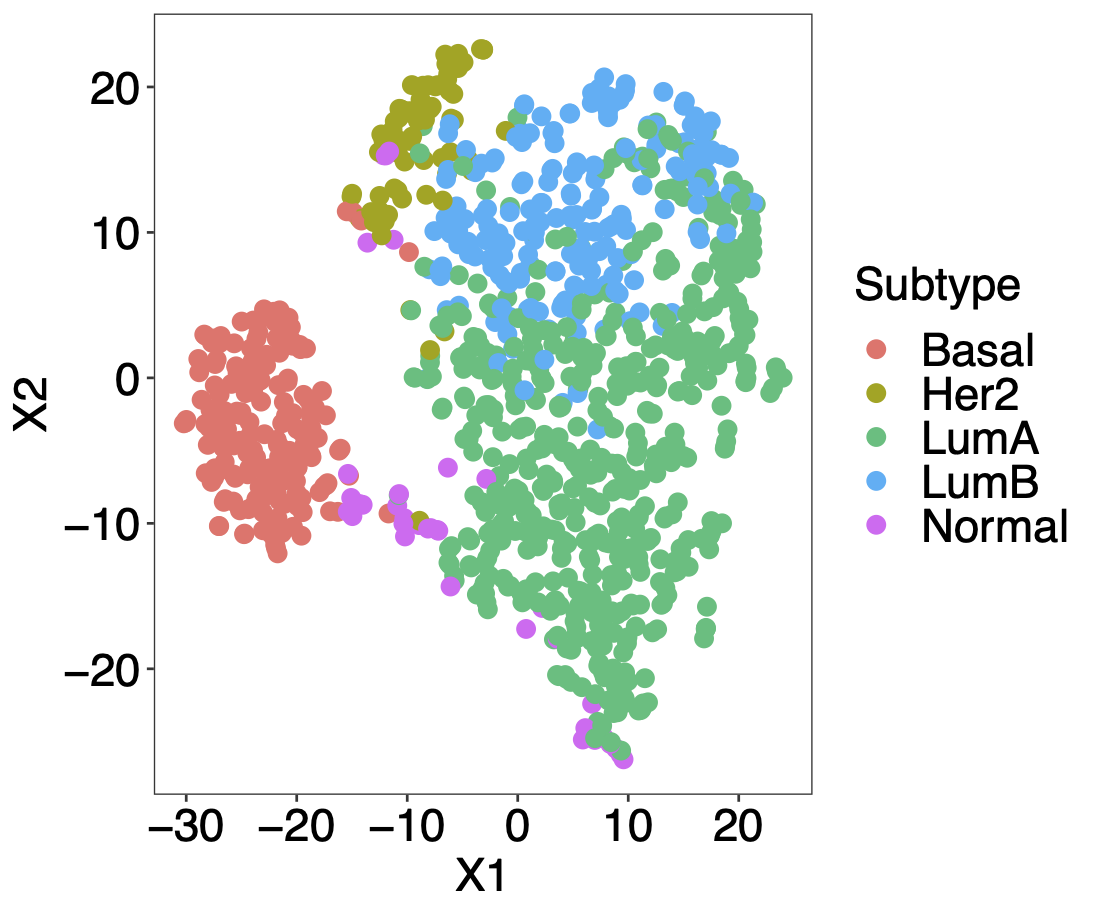
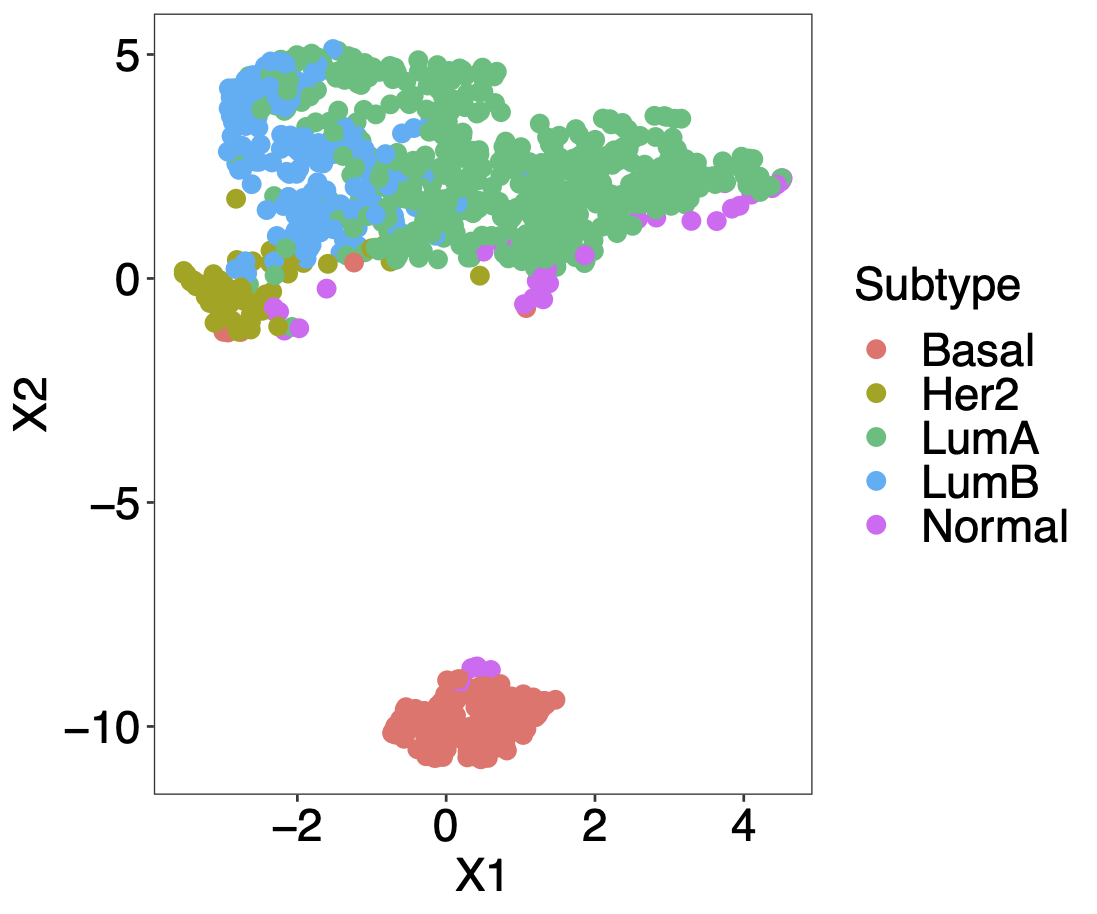
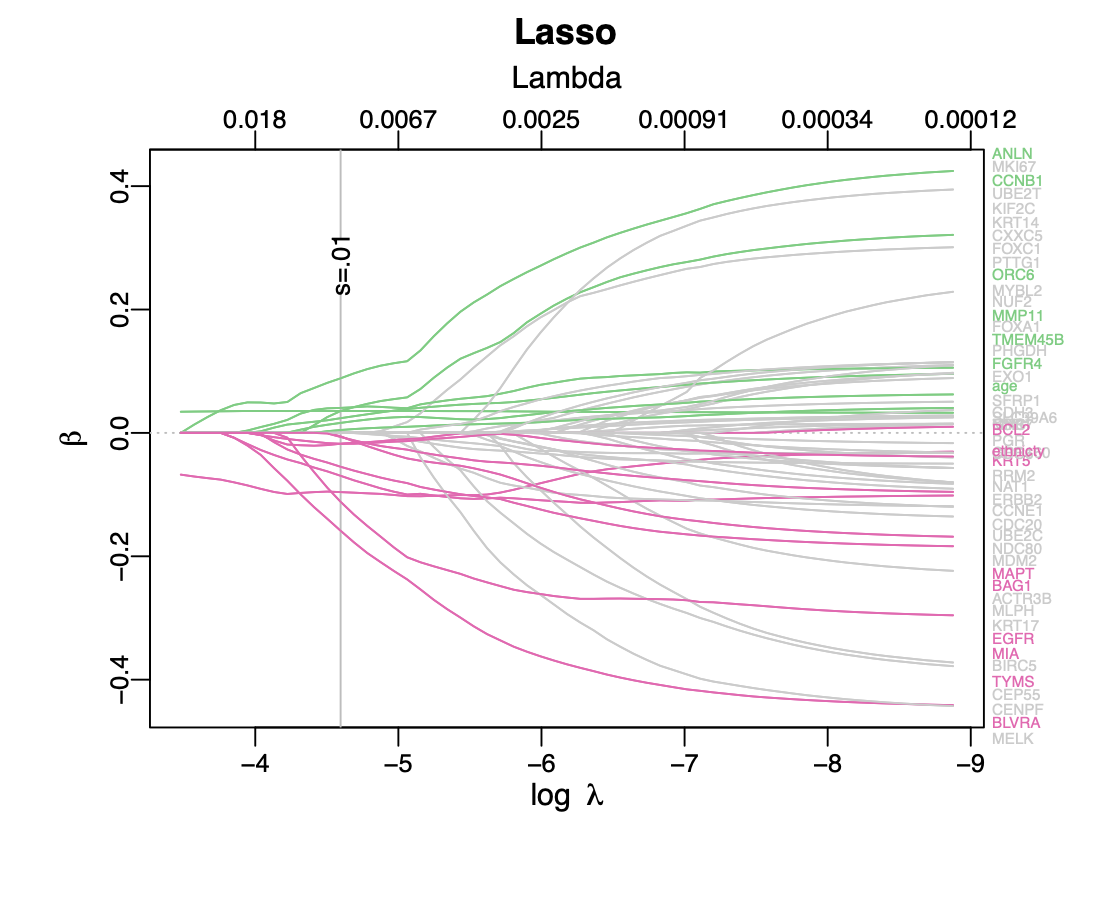
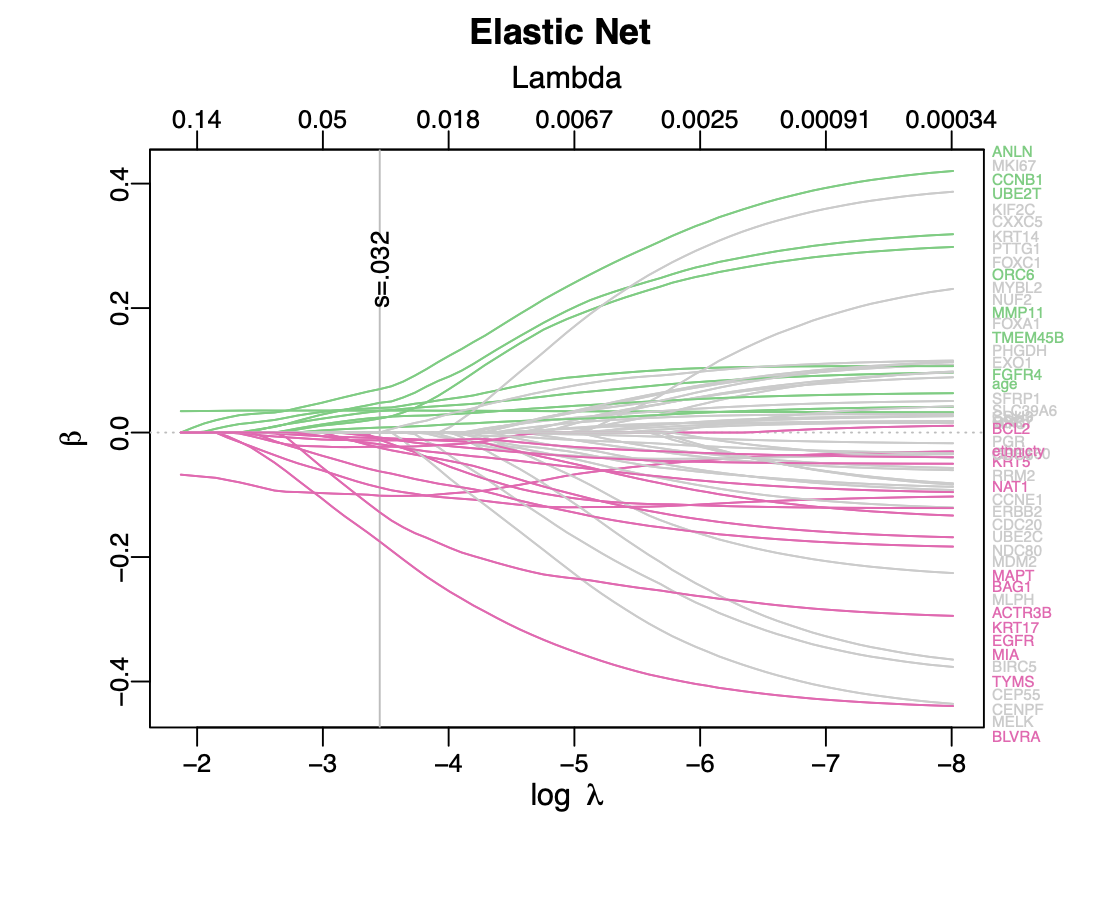
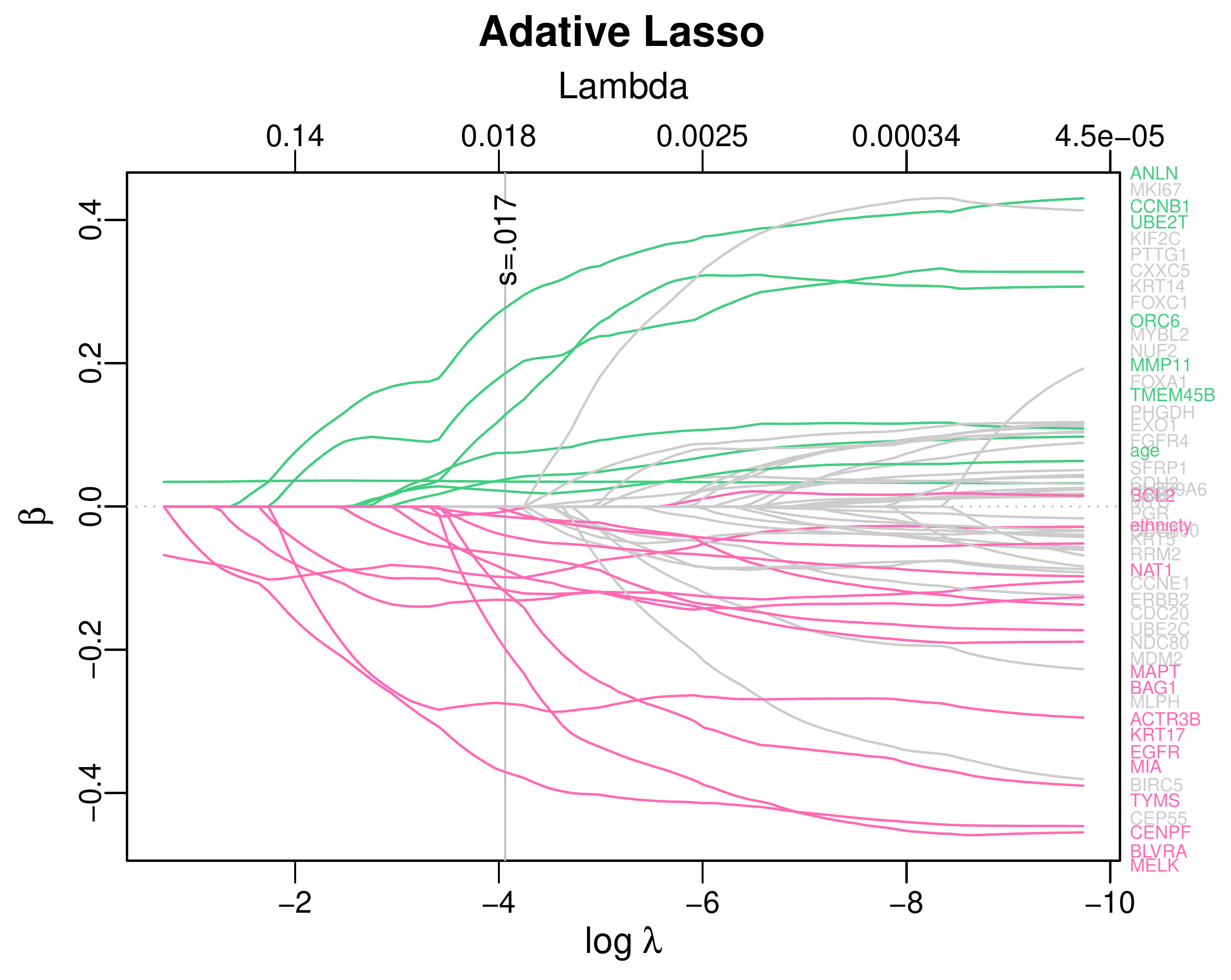
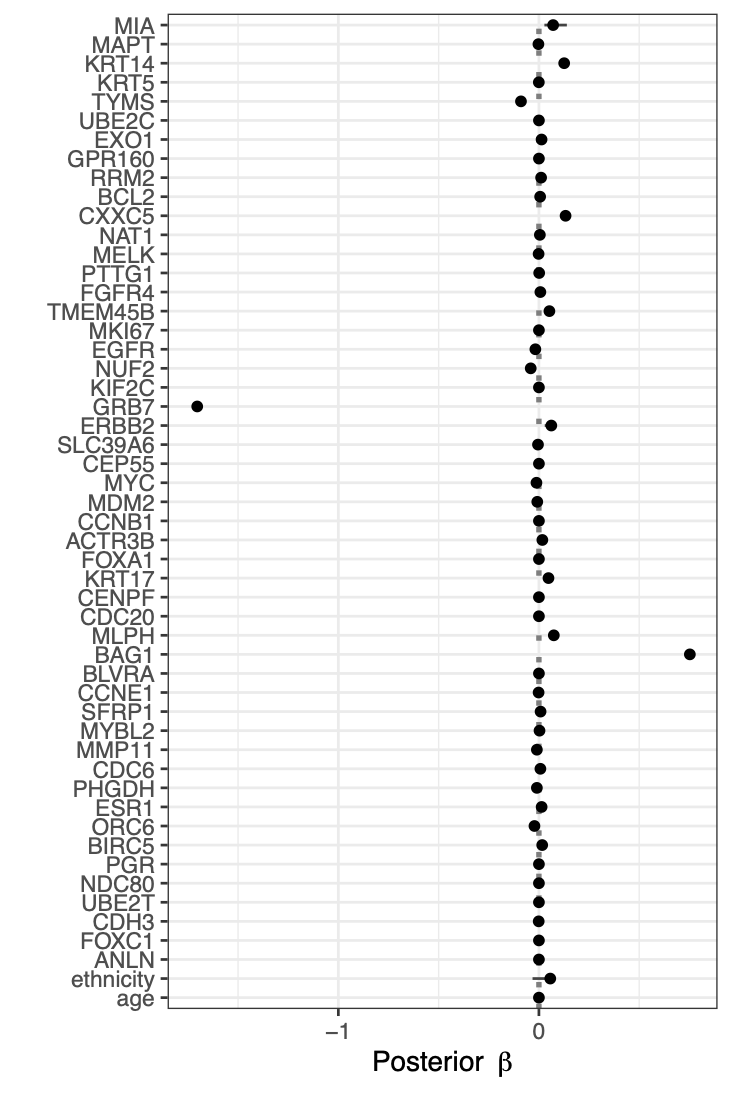
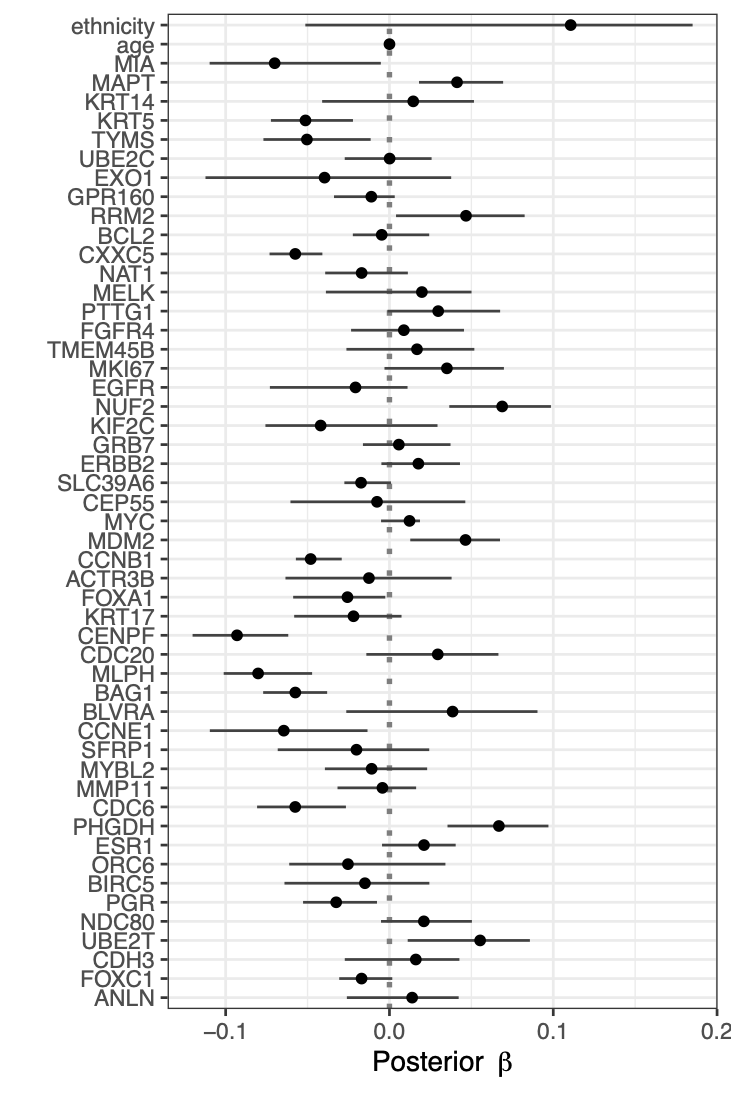
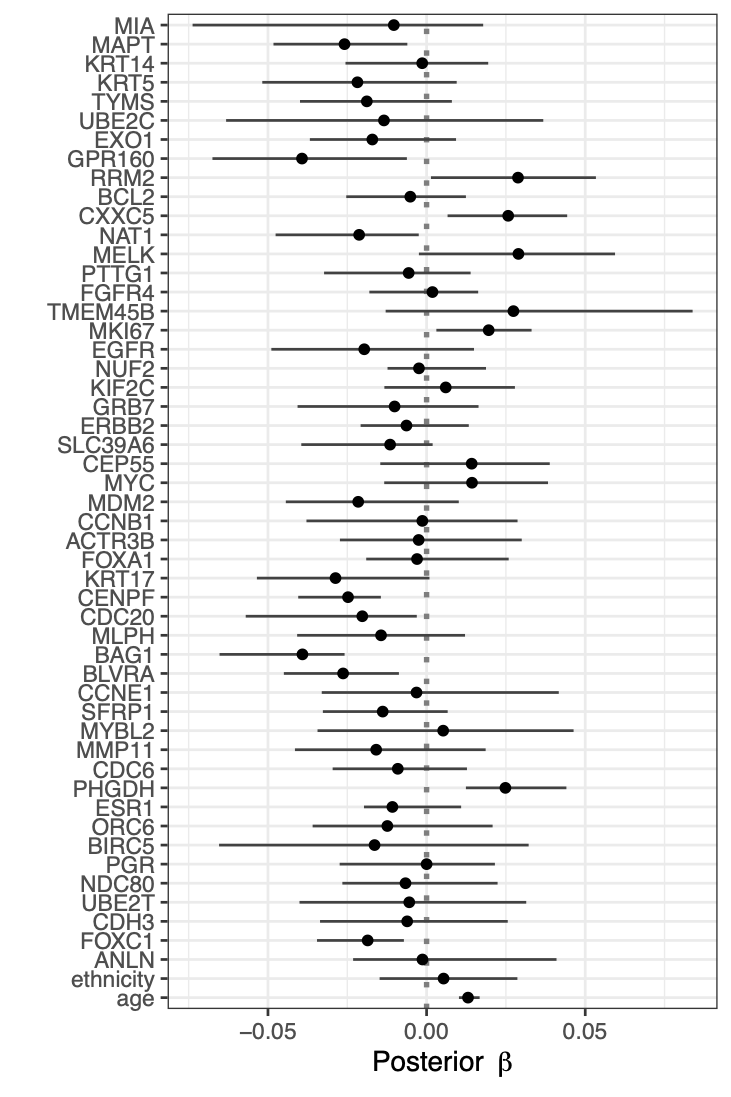
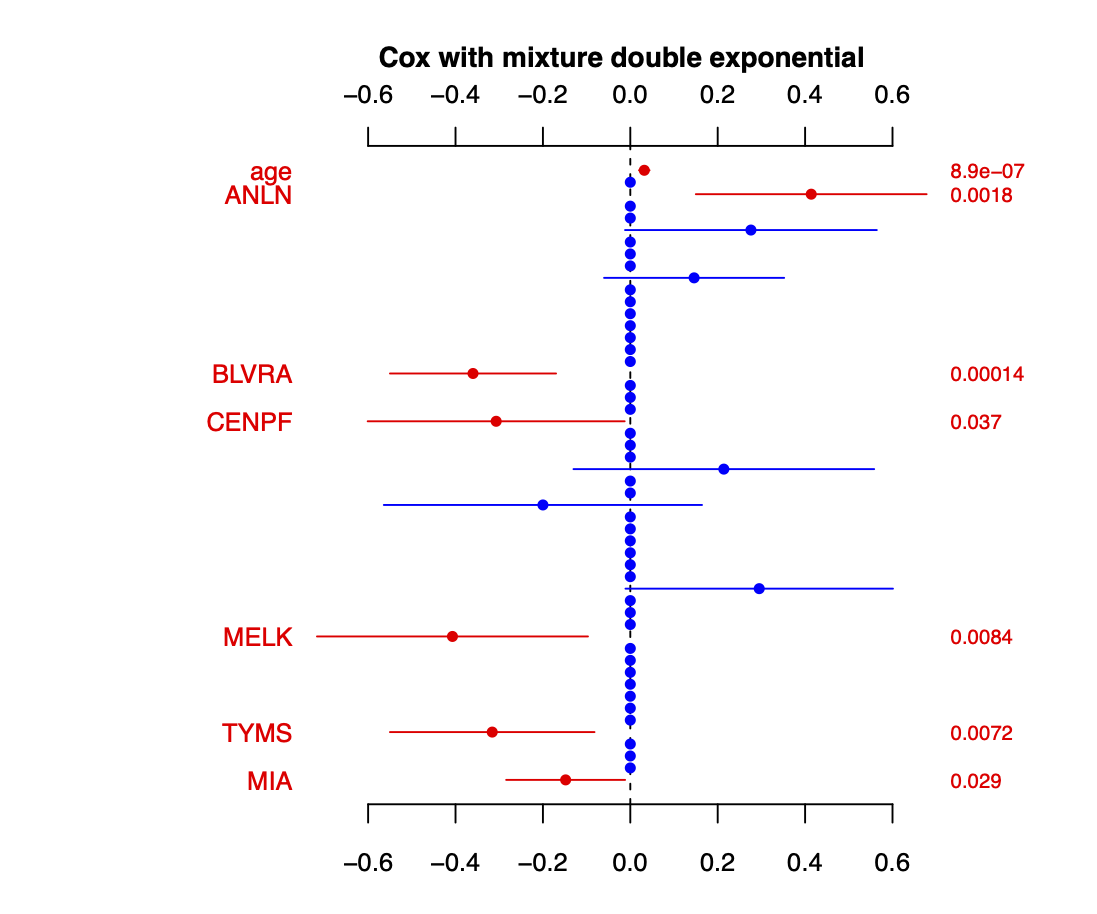
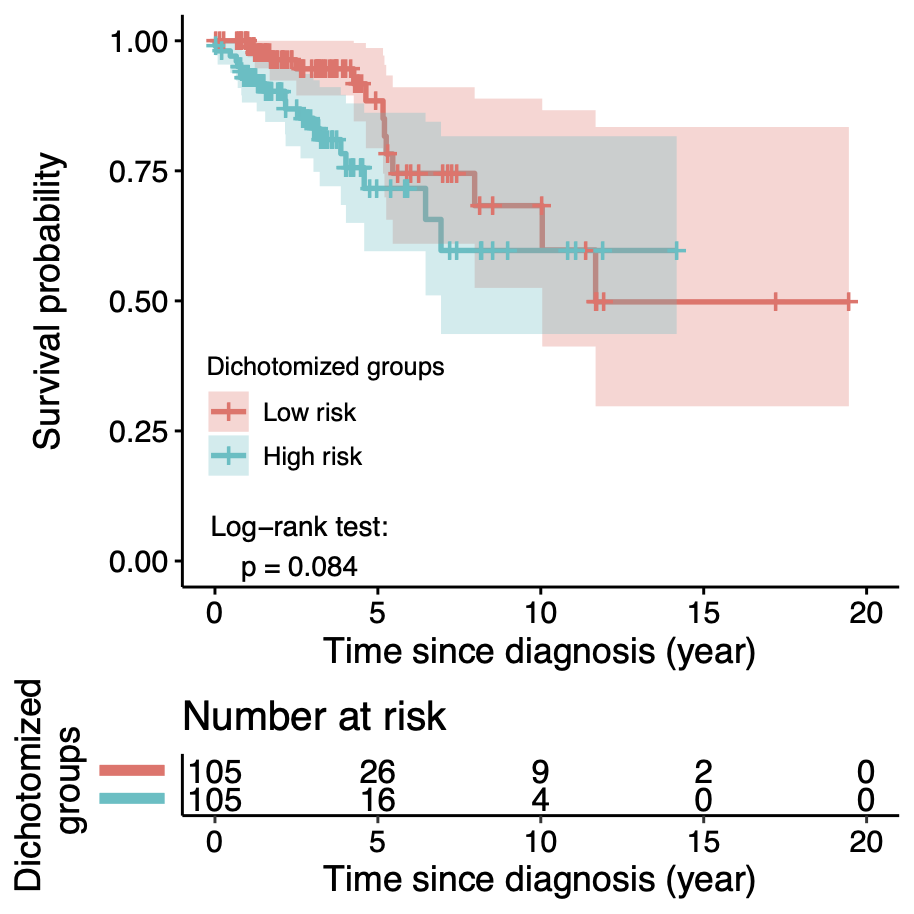
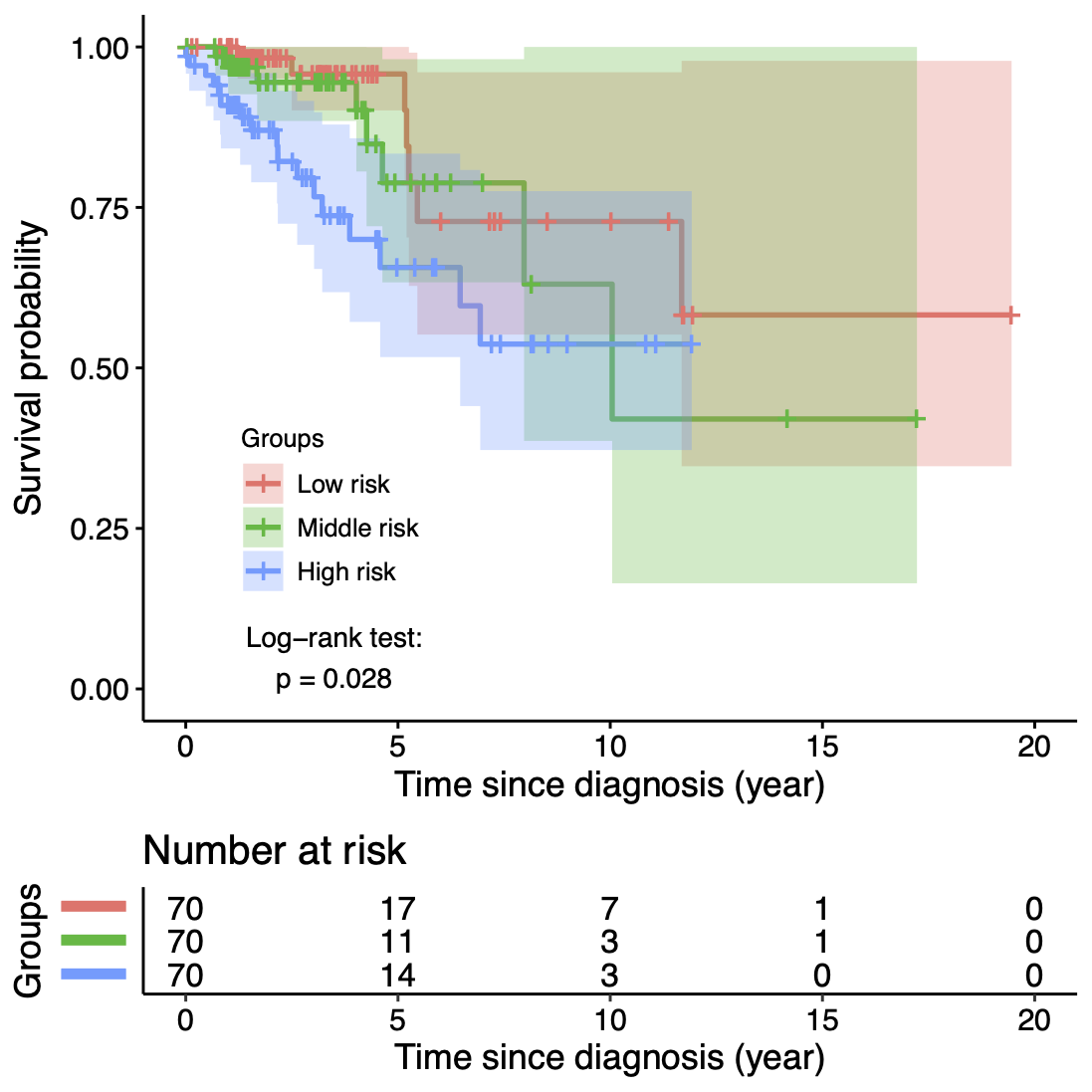
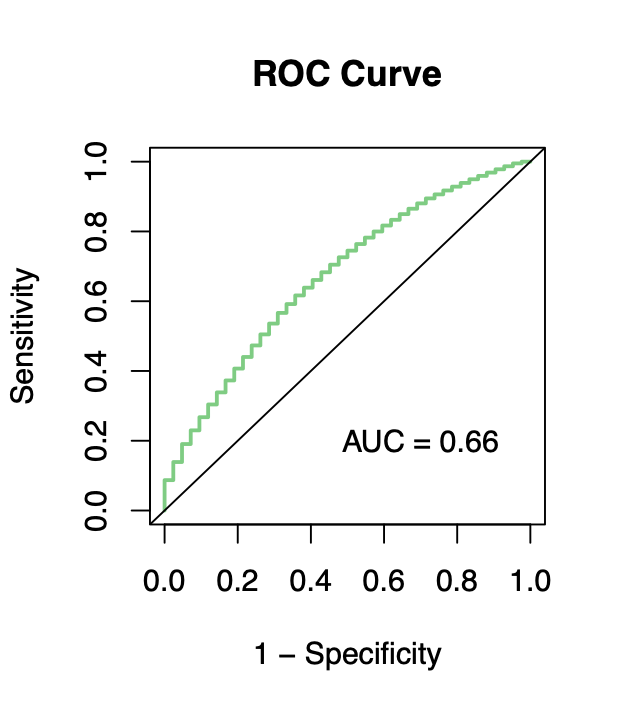
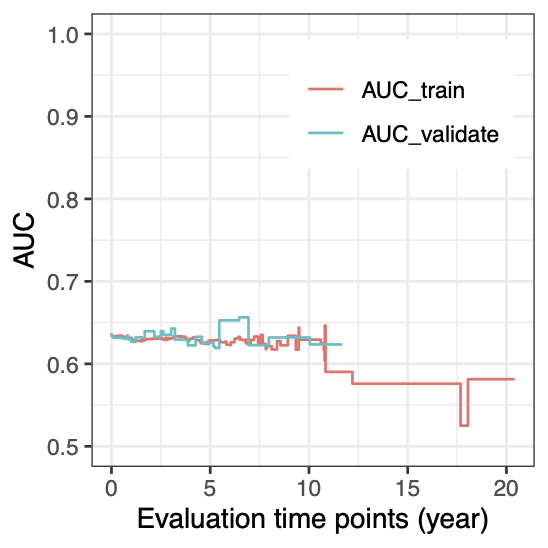
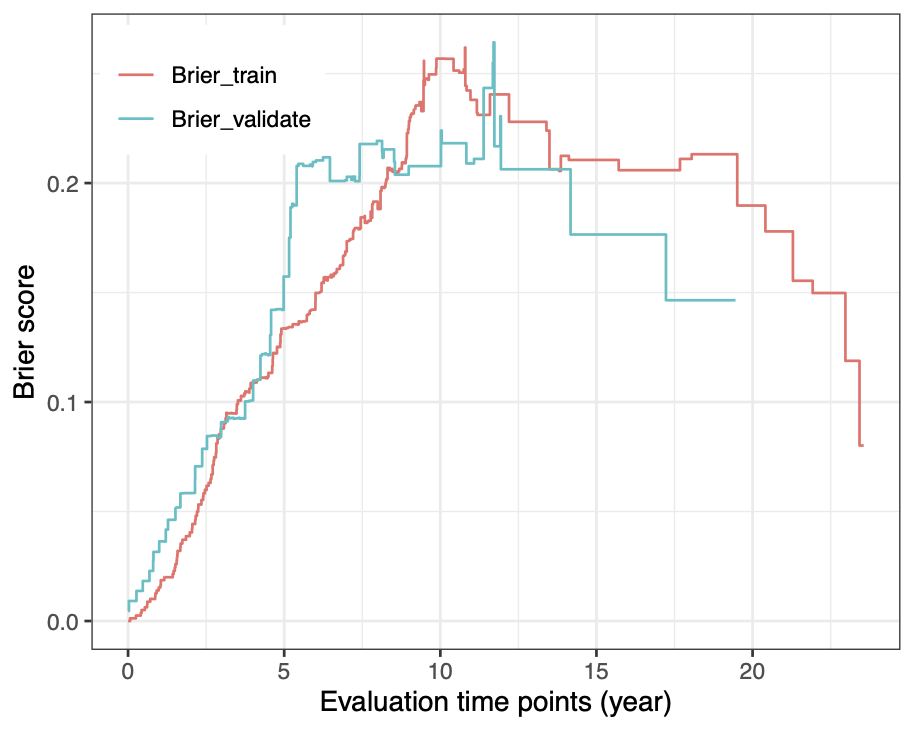
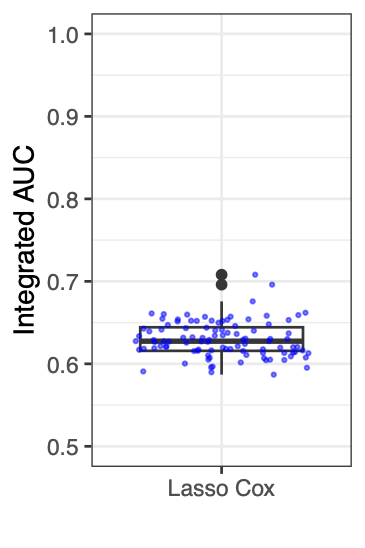
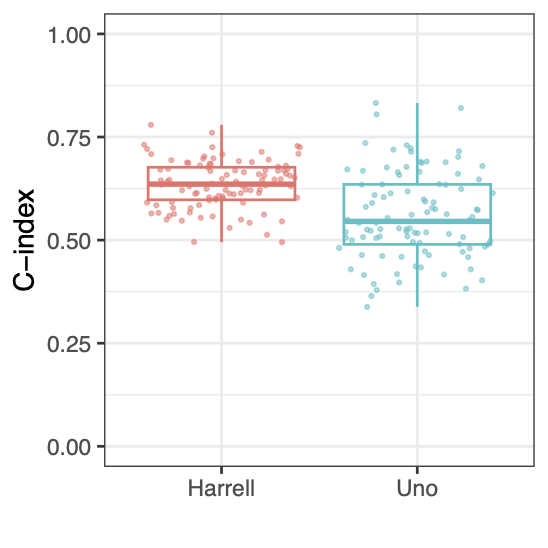
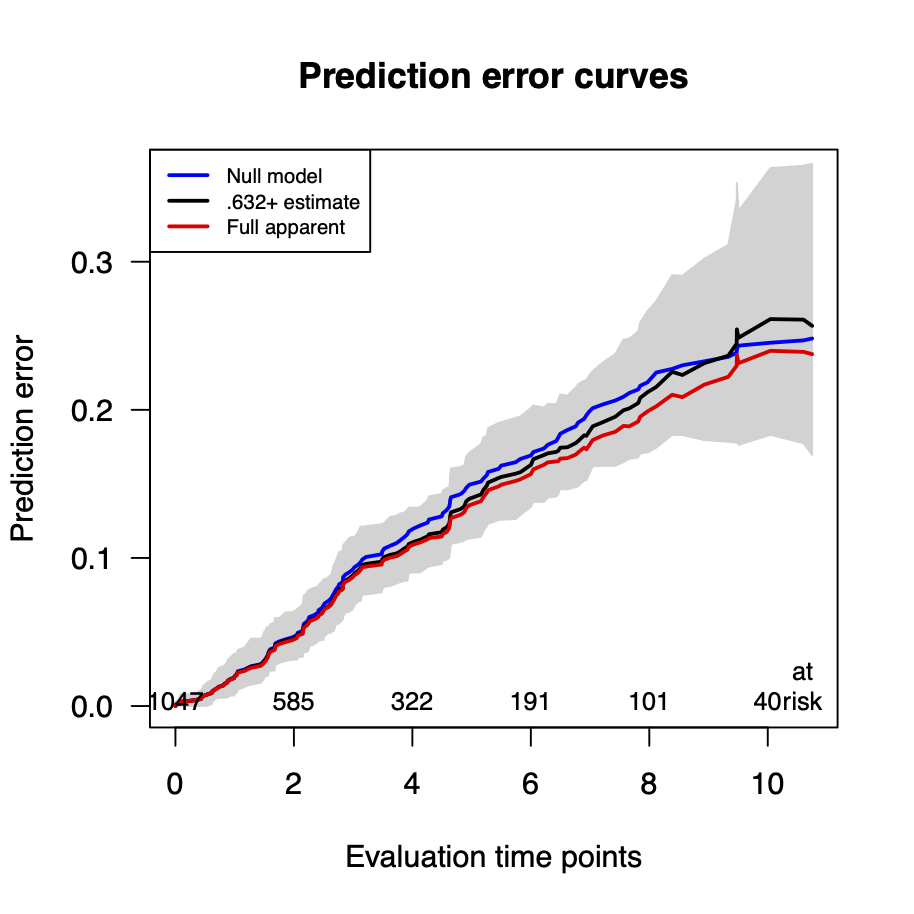
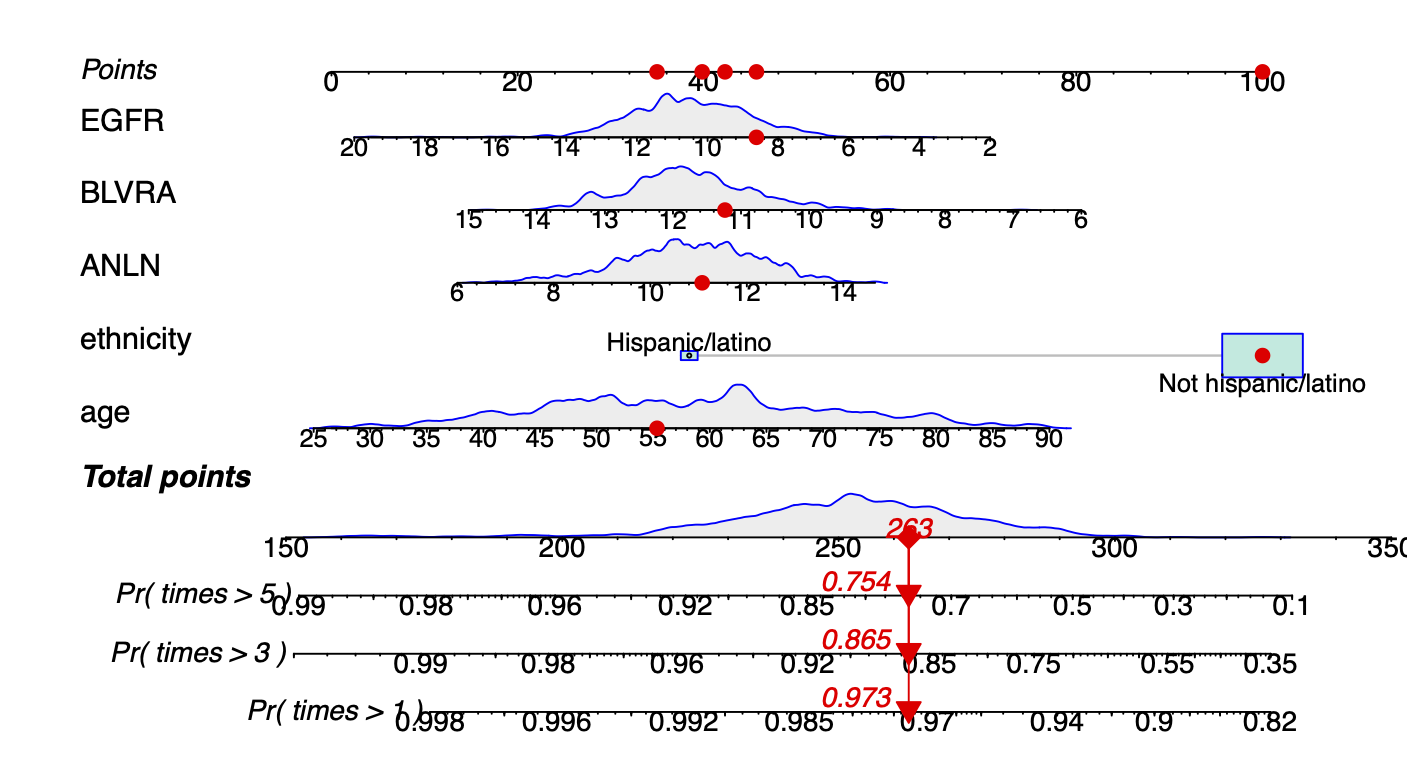
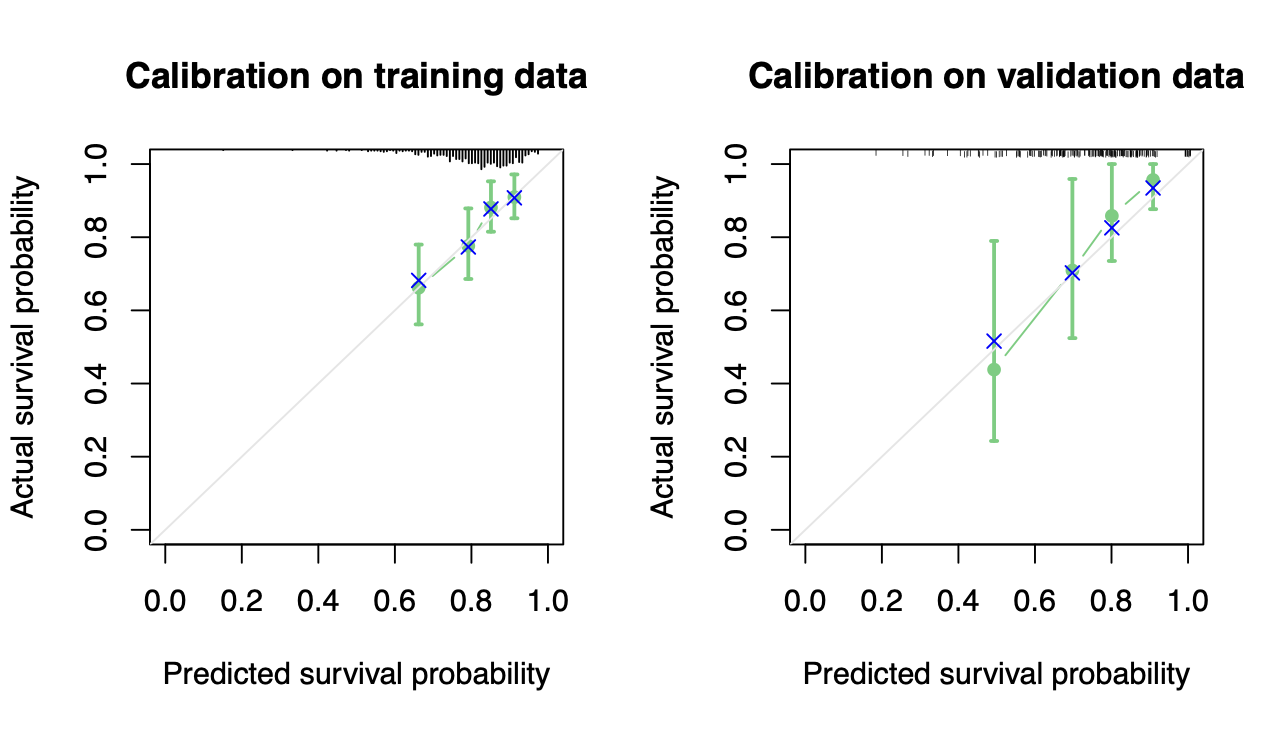
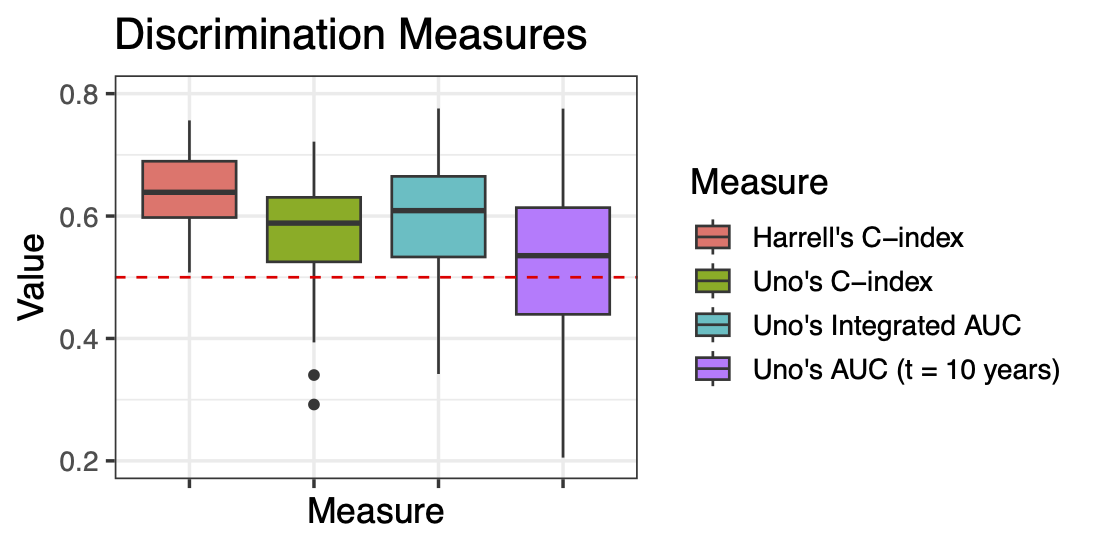
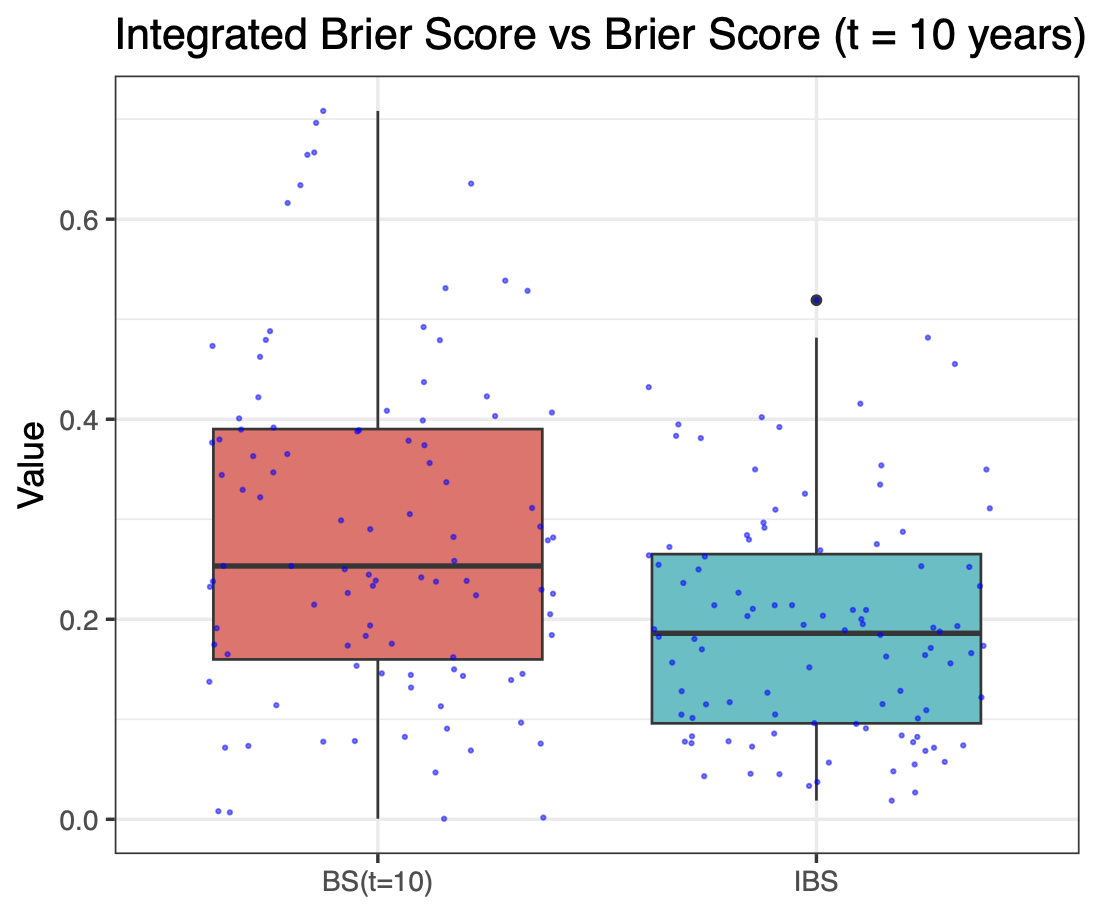
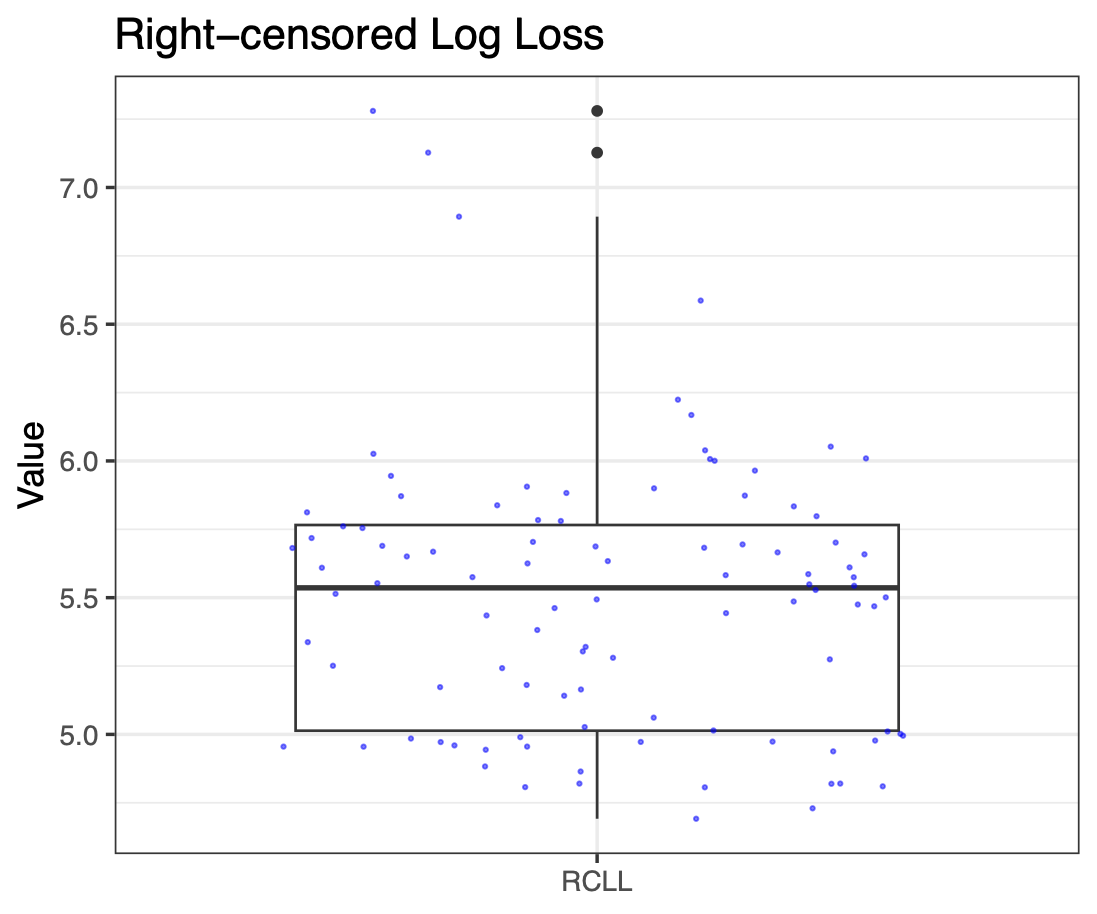 Calibration performance of Lasso Cox on the TCGA-BRCA dataset (expression data of the PAM50 genes and the variables age and ethnicity). Performance metrics used are the Integrated Brier Score (IBS), the Brier Score at 10 years and the Right-Censored Logarithmic Loss (RCLL). The dataset was split to training/validation sets 100 times to allow for the quantification of uncertainty in the different performance estimates.
Calibration performance of Lasso Cox on the TCGA-BRCA dataset (expression data of the PAM50 genes and the variables age and ethnicity). Performance metrics used are the Integrated Brier Score (IBS), the Brier Score at 10 years and the Right-Censored Logarithmic Loss (RCLL). The dataset was split to training/validation sets 100 times to allow for the quantification of uncertainty in the different performance estimates.